Applying logistic regression and SVM#

In this chapter you will learn the basics of applying logistic regression and support vector machines (SVMs) to classification problems. You’ll use the scikit-learn library to fit classification models to real data.

scikit-learn refresher#

KNN classification#

In this exercise you’ll explore a subset of the Large Movie Review Dataset. The variables X_train, X_test, y_train, and y_test are already loaded into the environment. The X variables contain features based on the words in the movie reviews, and the y variables contain labels for whether the review sentiment is positive (+1) or negative (-1).

This course touches on a lot of concepts you may have forgotten, so if you ever need a quick refresher, download the scikit-learn Cheat Sheet and keep it handy!

Create a KNN model with default hyperparameters.

Fit the model.

Print out the prediction for the test example 0.

# edited/added
import numpy as np
from sklearn.datasets import load_svmlight_file
X_train, y_train = load_svmlight_file('archive/Linear-Classifiers-in-Python/datasets/train_labeledBow.feat')
X_test, y_test = load_svmlight_file('archive/Linear-Classifiers-in-Python/datasets/test_labeledBow.feat')
X_train = X_train[11000:13000,:2500]
y_train = y_train[11000:13000]
y_train[y_train < 5] = -1.0
y_train[y_train >= 5] = 1.0
X_test = X_test[11000:13000,:2500]
y_test = y_test[11000:13000]
y_test[y_train < 5] = -1.0
y_test[y_train >= 5] = 1.0

from sklearn.neighbors import KNeighborsClassifier

# Create and fit the model
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)


# Predict on the test features, print the results

## KNeighborsClassifier()

pred = knn.predict(X_test)[0]
print("Prediction for test example 0:", pred)

## Prediction for test example 0: 1.0

Nice work! Looks like you remember how to use scikit-learn for supervised learning.

Comparing models#

Compare k nearest neighbors classifiers with k=1 and k=5 on the handwritten digits data set, which is already loaded into the variables X_train, y_train, X_test, and y_test. You can set k with the n_neighbors parameter when creating the KNeighborsClassifier object, which is also already imported into the environment.

Which model has a higher test accuracy?

# Create and fit the model
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)

## KNeighborsClassifier(n_neighbors=1)

knn.score(X_test, y_test)

# Predict on the test features, print the results

## 0.1645

pred = knn.predict(X_test)[0]
print("Prediction for test example 0:", pred)

# Create and fit the model

## Prediction for test example 0: 1.0

knn = KNeighborsClassifier()
knn.fit(X_train, y_train)

## KNeighborsClassifier()

knn.score(X_test, y_test)

# Predict on the test features, print the results

## 0.056

pred = knn.predict(X_test)[0]
print("Prediction for test example 0:", pred)

## Prediction for test example 0: 1.0

Great! You’ve just done a bit of model selection!

Overfitting#

Which of the following situations looks like an example of overfitting?

Training accuracy 50%, testing accuracy 50%.
Training accuracy 95%, testing accuracy 95%.
Training accuracy 95%, testing accuracy 50%.
Training accuracy 50%, testing accuracy 95%.

Great job! Looks like you understand overfitting.

Applying logistic regression and SVM#

Running LogisticRegression and SVC#

In this exercise, you’ll apply logistic regression and a support vector machine to classify images of handwritten digits.

Apply logistic regression and SVM (using SVC()) to the handwritten digits data set using the provided train/validation split.

For each classifier, print out the training and validation accuracy.

# edited/added
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn import datasets
digits = datasets.load_digits()
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target)

# Apply logistic regression and print scores
lr = LogisticRegression()
lr.fit(X_train, y_train)

## LogisticRegression()
## 
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/linear_model/_logistic.py:814: ConvergenceWarning: lbfgs failed to converge (status=1):
## STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
## 
## Increase the number of iterations (max_iter) or scale the data as shown in:
##     https://scikit-learn.org/stable/modules/preprocessing.html
## Please also refer to the documentation for alternative solver options:
##     https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
##   n_iter_i = _check_optimize_result(

print(lr.score(X_train, y_train))

## 1.0

print(lr.score(X_test, y_test))

# Apply SVM and print scores

## 0.9488888888888889

svm = SVC()
svm.fit(X_train, y_train)

## SVC()

print(svm.score(X_train, y_train))

## 0.994060876020787

print(svm.score(X_test, y_test))

## 0.9844444444444445

Nicely done! Later in the course we’ll look at the similarities and differences of logistic regression vs. SVMs.

Sentiment analysis for movie reviews#

In this exercise you’ll explore the probabilities outputted by logistic regression on a subset of the Large Movie Review Dataset.

The variables X and y are already loaded into the environment. X contains features based on the number of times words appear in the movie reviews, and y contains labels for whether the review sentiment is positive (+1) or negative (-1).

Train a logistic regression model on the movie review data.

Predict the probabilities of negative vs. positive for the two given reviews.

Feel free to write your own reviews and get probabilities for those too!

# edited/added
import numpy as np
import pandas as pd
from sklearn.datasets import load_svmlight_file
X, y = load_svmlight_file('archive/Linear-Classifiers-in-Python/datasets/train_labeledBow.feat')
X = X[11000:13000,:2500]
y = y[11000:13000]
y[y < 5] = -1.0
y[y >= 5] = 1.0
vocab = pd.read_csv('archive/Linear-Classifiers-in-Python/datasets/vocab.csv')['0'].values.tolist()
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(vocabulary = vocab)
def get_features(review):
    return vectorizer.transform([review])
  
# Instantiate logistic regression and train
lr = LogisticRegression()
lr.fit(X, y)

# Predict sentiment for a glowing review

## LogisticRegression()
## 
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/linear_model/_logistic.py:814: ConvergenceWarning: lbfgs failed to converge (status=1):
## STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
## 
## Increase the number of iterations (max_iter) or scale the data as shown in:
##     https://scikit-learn.org/stable/modules/preprocessing.html
## Please also refer to the documentation for alternative solver options:
##     https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
##   n_iter_i = _check_optimize_result(

review1 = "LOVED IT! This movie was amazing. Top 10 this year."
review1_features = get_features(review1)
print("Review:", review1)

## Review: LOVED IT! This movie was amazing. Top 10 this year.

print("Probability of positive review:", lr.predict_proba(review1_features)[0,1])

# Predict sentiment for a poor review

## Probability of positive review: 0.8807769884058808

review2 = "Total junk! I'll never watch a film by that director again, no matter how good the reviews."
review2_features = get_features(review2)
print("Review:", review2)

## Review: Total junk! I'll never watch a film by that director again, no matter how good the reviews.

print("Probability of positive review:", lr.predict_proba(review2_features)[0,1])

## Probability of positive review: 0.9086001000263592

Fantastic! The second probability would have been even lower, but the word “good” trips it up a bit, since that’s considered a “positive” word.

Linear classifiers#

Which decision boundary is linear?#

Which of the following is a linear decision boundary?

Good job! You correctly identified the linear decision boundary.

Visualizing decision boundaries#

In this exercise, you’ll visualize the decision boundaries of various classifier types.

A subset of scikit-learn’s built-in wine dataset is already loaded into X, along with binary labels in y.

Create the following classifier objects with default hyperparameters: LogisticRegression, LinearSVC, SVC, KNeighborsClassifier.

Fit each of the classifiers on the provided data using a for loop.

Call the plot_4\_classifers() function (similar to the code here), passing in X, y, and a list containing the four classifiers.

# edited/added
import matplotlib.pyplot as plt
X = np.array([[11.45,  2.4 ],
       [13.62,  4.95],
       [13.88,  1.89],
       [12.42,  2.55],
       [12.81,  2.31],
       [12.58,  1.29],
       [13.83,  1.57],
       [13.07,  1.5 ],
       [12.7 ,  3.55],
       [13.77,  1.9 ],
       [12.84,  2.96],
       [12.37,  1.63],
       [13.51,  1.8 ],
       [13.87,  1.9 ],
       [12.08,  1.39],
       [13.58,  1.66],
       [13.08,  3.9 ],
       [11.79,  2.13],
       [12.45,  3.03],
       [13.68,  1.83],
       [13.52,  3.17],
       [13.5 ,  3.12],
       [12.87,  4.61],
       [14.02,  1.68],
       [12.29,  3.17],
       [12.08,  1.13],
       [12.7 ,  3.87],
       [11.03,  1.51],
       [13.32,  3.24],
       [14.13,  4.1 ],
       [13.49,  1.66],
       [11.84,  2.89],
       [13.05,  2.05],
       [12.72,  1.81],
       [12.82,  3.37],
       [13.4 ,  4.6 ],
       [14.22,  3.99],
       [13.72,  1.43],
       [12.93,  2.81],
       [11.64,  2.06],
       [12.29,  1.61],
       [11.65,  1.67],
       [13.28,  1.64],
       [12.93,  3.8 ],
       [13.86,  1.35],
       [11.82,  1.72],
       [12.37,  1.17],
       [12.42,  1.61],
       [13.9 ,  1.68],
       [14.16,  2.51]])
y = np.array([ True,  True, False,  True,  True,  True, False, False,  True,
       False,  True,  True, False, False,  True, False,  True,  True,
        True, False,  True,  True,  True, False,  True,  True,  True,
        True,  True,  True,  True,  True, False,  True,  True,  True,
       False, False,  True,  True,  True,  True, False, False, False,
        True,  True,  True, False,  True])
        
def make_meshgrid(x, y, h=.02, lims=None):
    """Create a mesh of points to plot in
    
    Parameters
    ----------
        x: data to base x-axis meshgrid on
        y: data to base y-axis meshgrid on
        h: stepsize for meshgrid, optional
        
    Returns
    -------
        xx, yy : ndarray
    """
    
    if lims is None:
        x_min, x_max = x.min() - 1, x.max() + 1
        y_min, y_max = y.min() - 1, y.max() + 1
    else:
        x_min, x_max, y_min, y_max = lims
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    return xx, yy
  
def plot_contours(ax, clf, xx, yy, proba=False, **params):
    """Plot the decision boundaries for a classifier.
    
    Parameters
    ----------
        ax: matplotlib axes object
        clf: a classifier
        xx: meshgrid ndarray
        yy: meshgrid ndarray
        params: dictionary of params to pass to contourf, optional
    """
    if proba:
        Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:,-1]
        Z = Z.reshape(xx.shape)
        out = ax.imshow(Z,extent=(np.min(xx), np.max(xx), np.min(yy), np.max(yy)), 
                        origin='lower', vmin=0, vmax=1, **params)
        ax.contour(xx, yy, Z, levels=[0.5])
    else:
        Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
        Z = Z.reshape(xx.shape)
        out = ax.contourf(xx, yy, Z, **params)
    return out
  
def plot_classifier(X, y, clf, ax=None, ticks=False, proba=False, lims=None): 
    # assumes classifier "clf" is already fit
    X0, X1 = X[:, 0], X[:, 1]
    xx, yy = make_meshgrid(X0, X1, lims=lims)
    
    if ax is None:
        plt.figure()
        ax = plt.gca()
        show = True
    else:
        show = False
        
    # can abstract some of this into a higher-level function for learners to call
    cs = plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8, proba=proba)
    if proba:
        cbar = plt.colorbar(cs)
        cbar.ax.set_ylabel('probability of red $\Delta$ class', fontsize=20, rotation=270, labelpad=30)
        cbar.ax.tick_params(labelsize=14)
        #ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=30, edgecolors=\'k\', linewidth=1)
    labels = np.unique(y)
    if len(labels) == 2:
        ax.scatter(X0[y==labels[0]], X1[y==labels[0]], cmap=plt.cm.coolwarm, 
                   s=60, c='b', marker='o', edgecolors='k')
        ax.scatter(X0[y==labels[1]], X1[y==labels[1]], cmap=plt.cm.coolwarm, 
                   s=60, c='r', marker='^', edgecolors='k')
    else:
        ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=50, edgecolors='k', linewidth=1)

    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    #     ax.set_xlabel(data.feature_names[0])
    #     ax.set_ylabel(data.feature_names[1])
    if ticks:
        ax.set_xticks(())
        ax.set_yticks(())
        #     ax.set_title(title)
    if show:
        plt.show()
    else:
        return ax
      
def plot_4_classifiers(X, y, clfs):
    # Set-up 2x2 grid for plotting.
    fig, sub = plt.subplots(2, 2)
    plt.subplots_adjust(wspace=0.2, hspace=0.2)
    
    for clf, ax, title in zip(clfs, sub.flatten(), ("(1)", "(2)", "(3)", "(4)")):
        # clf.fit(X, y)
        plot_classifier(X, y, clf, ax, ticks=True)
        ax.set_title(title)

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.neighbors import KNeighborsClassifier

# Define the classifiers
classifiers = [LogisticRegression(), LinearSVC(),
               SVC(), KNeighborsClassifier()]
               
# Fit the classifiers
for c in classifiers:
    c.fit(X, y)
    
# Plot the classifiers

## LogisticRegression()
## LinearSVC()
## SVC()
## KNeighborsClassifier()
## 
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/svm/_base.py:1199: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
##   warnings.warn(

plot_4_classifiers(X, y, classifiers)
plt.show()

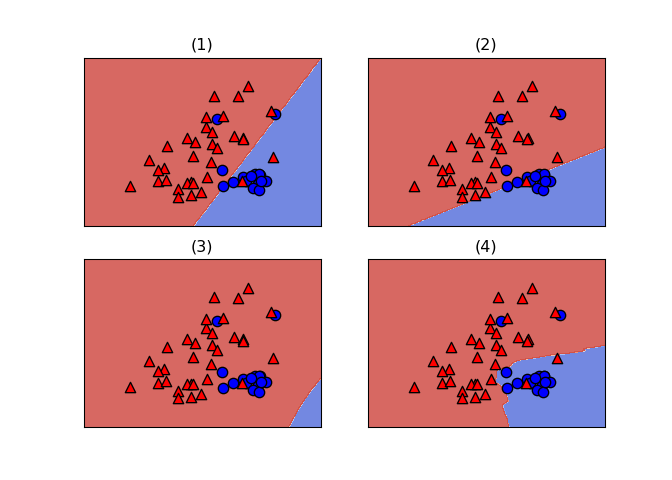
Nice! As you can see, logistic regression and linear SVM are linear classifiers whereas KNN is not. The default SVM is also non-linear, but this is hard to see in the plot because it performs poorly with default hyperparameters. With better hyperparameters, it performs well.

Machine Learning Scientist with Python

Applying logistic regression and SVM

Contents

Applying logistic regression and SVM#

scikit-learn refresher#

KNN classification#

Comparing models#

Overfitting#

Applying logistic regression and SVM#

Running LogisticRegression and SVC#

Sentiment analysis for movie reviews#

Linear classifiers#

Which decision boundary is linear?#

Visualizing decision boundaries#