The Bias-Variance Tradeoff#

The bias-variance tradeoff is one of the fundamental concepts in supervised machine learning. In this chapter, you’ll understand how to diagnose the problems of overfitting and underfitting. You’ll also be introduced to the concept of ensembling where the predictions of several models are aggregated to produce predictions that are more robust.

Generalization Error#

Complexity, bias and variance#

In the video, you saw how the complexity of a model labeled f^ influences the bias and variance terms of its generalization error.
Which of the following correctly describes the relationship between f^’s complexity and f^’s bias and variance terms?

  • As the complexity of f^ decreases, the bias term decreases while the variance term increases.

  • As the complexity of f^ decreases, both the bias and the variance terms increase.

  • As the complexity of f^ increases, the bias term increases while the variance term decreases.

  • As the complexity of f^ increases, the bias term decreases while the variance term increases.

Great work! You’re now able to relate model complexity to bias and variance!

Overfitting and underfitting#

In this exercise, you’ll visually diagnose whether a model is overfitting or underfitting the training set.

For this purpose, we have trained two different models A and B on the auto dataset to predict the mpg consumption of a car using only the car’s displacement (displ) as a feature.

The following figure shows you scatterplots of mpg versus displ along with lines corresponding to the training set predictions of models A and B in red.

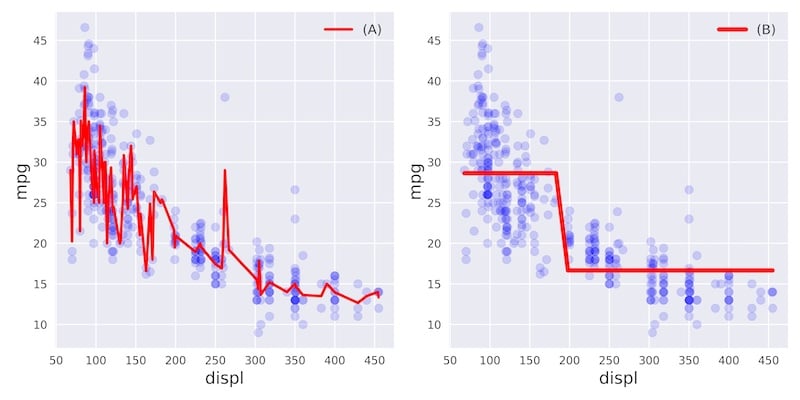
diagnose

Which of the following statements is true?

  • [ ] A suffers from high bias and overfits the training set.

  • [ ] A suffers from high variance and underfits the training set.

  • [x] B suffers from high bias and underfits the training set.

  • [ ] B suffers from high variance and underfits the training set.

Absolutely! Model B is not able to capture the nonlinear dependence of mpg on displ.

Diagnose bias and variance problems#

Instantiate the model#

In the following set of exercises, you’ll diagnose the bias and variance problems of a regression tree. The regression tree you’ll define in this exercise will be used to predict the mpg consumption of cars from the auto dataset using all available features.

We have already processed the data and loaded the features matrix X and the array y in your workspace. In addition, the DecisionTreeRegressor class was imported from sklearn.tree.

  • Import train_test_split from sklearn.model_selection.
  • Split the data into 70% train and 30% test.
  • Instantiate a DecisionTreeRegressor with max depth 4 and min_samples_leaf set to 0.26. 
    • # Import train_test_split from sklearn.model_selection
from sklearn.model_selection import train_test_split

# Set SEED for reproducibility
SEED = 1

# Split the data into 70% train and 30% test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=SEED)

# Instantiate a DecisionTreeRegressor dt
dt = DecisionTreeRegressor(max_depth=4, min_samples_leaf=0.26, random_state=SEED)

    Great work! In the next exercise, you’ll evaluate dt’s CV error.

    Evaluate the 10-fold CV error#

    In this exercise, you’ll evaluate the 10-fold CV Root Mean Squared Error (RMSE) achieved by the regression tree dt that you instantiated in the previous exercise.

    In addition to dt, the training data including X_train and y_train are available in your workspace. We also imported cross_val_score from sklearn.model_selection.

    Note that since cross_val_score has only the option of evaluating the negative MSEs, its output should be multiplied by negative one to obtain the MSEs. The CV RMSE can then be obtained by computing the square root of the average MSE.

  • Compute dt‘s 10-fold cross-validated MSE by setting the scoring argument to ’neg_mean_squared_error’.
  • Compute RMSE from the obtained MSE scores. 
    • # edited/added
from sklearn.model_selection import cross_val_score

# Compute the array containing the 10-folds CV MSEs
MSE_CV_scores = - cross_val_score(dt, X_train, y_train, cv=10, 
                                  scoring='neg_mean_squared_error', 
                                  n_jobs=-1) 
                                  
# Compute the 10-folds CV RMSE
RMSE_CV = (MSE_CV_scores.mean())**(1/2)

# Print RMSE_CV
print('CV RMSE: {:.2f}'.format(RMSE_CV))

    ## CV RMSE: 5.14

    Great work! A very good practice is to keep the test set untouched until you are confident about your model’s performance. CV is a great technique to get an estimate of a model’s performance without affecting the test set.

    Evaluate the training error#

    You’ll now evaluate the training set RMSE achieved by the regression tree dt that you instantiated in a previous exercise.

    In addition to dt, X_train and y_train are available in your workspace.

    Note that in scikit-learn, the MSE of a model can be computed as follows: 

    MSE_model = mean_squared_error(y_true, y_predicted)

    where we use the function mean_squared_error from the metrics module and pass it the true labels y_true as a first argument, and the predicted labels from the model y_predicted as a second argument.

  • Import mean_squared_error as MSE from sklearn.metrics.
  • Fit dt to the training set.
  • Predict dt’s training set labels and assign the result to y_pred_train.
  • Evaluate dt’s training set RMSE and assign it to RMSE_train. 
    • # Import mean_squared_error from sklearn.metrics as MSE
from sklearn.metrics import mean_squared_error as MSE

# Fit dt to the training set
dt.fit(X_train, y_train)

# Predict the labels of the training set

    ## DecisionTreeRegressor(max_depth=4, min_samples_leaf=0.26, random_state=1)

    y_pred_train = dt.predict(X_train)

# Evaluate the training set RMSE of dt
RMSE_train = (MSE(y_train, y_pred_train))**(1/2)

# Print RMSE_train
print('Train RMSE: {:.2f}'.format(RMSE_train))

    ## Train RMSE: 5.15

    Awesome! Notice how the training error is roughly equal to the 10-folds CV error you obtained in the previous exercise.

    High bias or high variance?#

    In this exercise you’ll diagnose whether the regression tree dt you trained in the previous exercise suffers from a bias or a variance problem.

    The training set RMSE (RMSE_train) and the CV RMSE (RMSE_CV) achieved by dt are available in your workspace. In addition, we have also loaded a variable called baseline_RMSE which corresponds to the root mean-squared error achieved by the regression-tree trained with the disp feature only (it is the RMSE achieved by the regression tree trained in chapter 1, lesson 3). Here baseline_RMSE serves as the baseline RMSE above which a model is considered to be underfitting and below which the model is considered ‘good enough’.

    Does dt suffer from a high bias or a high variance problem?

    • dt suffers from high variance because RMSE_CV is far less than RMSE_train.

    • dt suffers from high bias because RMSE_CV ≈ RMSE_train and both scores are greater than baseline_RMSE.

    • dt is a good fit because RMSE_CV ≈ RMSE_train and both scores are smaller than baseline_RMSE.

    Correct! dt is indeed underfitting the training set as the model is too constrained to capture the nonlinear dependencies between features and labels.

    Ensemble Learning#

    Define the ensemble#

    In the following set of exercises, you’ll work with the Indian Liver Patient Dataset from the UCI Machine learning repository.

    In this exercise, you’ll instantiate three classifiers to predict whether a patient suffers from a liver disease using all the features present in the dataset.

    The classes LogisticRegression, DecisionTreeClassifier, and KNeighborsClassifier under the alias KNN are available in your workspace.

  • Instantiate a Logistic Regression classifier and assign it to lr.
  • Instantiate a KNN classifier that considers 27 nearest neighbors and assign it to knn.
  • Instantiate a Decision Tree Classifier with the parameter min_samples_leaf set to 0.13 and assign it to dt. 
    • # edited/added
df = pd.read_csv("archive/Machine-Learning-with-Tree-Based-Models-in-Python/datasets/indian_liver_patient_preprocessed.csv")
X = df.drop(columns = ['Liver_disease'])
y = df['Liver_disease']
X_train, X_test,  y_train, y_test = sklearn.model_selection.train_test_split(X,y)
from sklearn.neighbors import KNeighborsClassifier

# Set seed for reproducibility
SEED=1

# Instantiate lr
lr = LogisticRegression(random_state=SEED)

# Instantiate knn
knn = KNeighborsClassifier(n_neighbors=27)

# Instantiate dt
dt = DecisionTreeClassifier(min_samples_leaf=.13, random_state=SEED)

# Define the list classifiers
classifiers = [('Logistic Regression', lr), ('K Nearest Neighbours', knn), ('Classification Tree', dt)]

    Great! In the next exercise, you will train these classifiers and evaluate their test set accuracy.

    Evaluate individual classifiers#

    In this exercise you’ll evaluate the performance of the models in the list classifiers that we defined in the previous exercise. You’ll do so by fitting each classifier on the training set and evaluating its test set accuracy.

    The dataset is already loaded and preprocessed for you (numerical features are standardized) and it is split into 70% train and 30% test. The features matrices X_train and X_test, as well as the arrays of labels y_train and y_test are available in your workspace. In addition, we have loaded the list classifiers from the previous exercise, as well as the function accuracy_score() from sklearn.metrics.

  • Iterate over the tuples in classifiers. Use clf_name and clf as the for loop variables:
  • Fit clf to the training set.
  • Predict clf’s test set labels and assign the results to y_pred.
  • Evaluate the test set accuracy of clf and print the result. 
    • from sklearn.metrics import accuracy_score

# Iterate over the pre-defined list of classifiers
for clf_name, clf in classifiers:    
 
    # Fit clf to the training set
    clf.fit(X_train, y_train)    
   
    # Predict y_pred
    y_pred = clf.predict(X_test)
    
    # Calculate accuracy
    accuracy = accuracy_score(y_test, y_pred) 
   
    # Evaluate clf's accuracy on the test set
    print('{:s} : {:.3f}'.format(clf_name, accuracy))

    ## LogisticRegression(random_state=1)
## Logistic Regression : 0.697
## KNeighborsClassifier(n_neighbors=27)
## K Nearest Neighbours : 0.676
## DecisionTreeClassifier(min_samples_leaf=0.13, random_state=1)
## Classification Tree : 0.703
## 
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/linear_model/_logistic.py:814: ConvergenceWarning: lbfgs failed to converge (status=1):
## STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
## 
## Increase the number of iterations (max_iter) or scale the data as shown in:
##     https://scikit-learn.org/stable/modules/preprocessing.html
## Please also refer to the documentation for alternative solver options:
##     https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
##   n_iter_i = _check_optimize_result(
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/base.py:441: UserWarning: X does not have valid feature names, but KNeighborsClassifier was fitted with feature names
##   warnings.warn(

    Great work! Notice how Logistic Regression achieved the highest accuracy of 74.1%.

    Better performance with a Voting Classifier#

    Finally, you’ll evaluate the performance of a voting classifier that takes the outputs of the models defined in the list classifiers and assigns labels by majority voting.

    X_train, X_test,y_train, y_test, the list classifiers defined in a previous exercise, as well as the function accuracy_score from sklearn.metrics are available in your workspace.

  • Import VotingClassifier from sklearn.ensemble.
  • Instantiate a VotingClassifier by setting the parameter estimators to classifiers and assign it to vc.
  • Fit vc to the training set.
  • Evaluate vc’s test set accuracy using the test set predictions y_pred. 
    • # Import VotingClassifier from sklearn.ensemble
from sklearn.ensemble import VotingClassifier

# Instantiate a VotingClassifier vc
vc = VotingClassifier(estimators=classifiers)

# Fit vc to the training set
vc.fit(X_train, y_train)

# Evaluate the test set predictions

    ## VotingClassifier(estimators=[('Logistic Regression',
##                               LogisticRegression(random_state=1)),
##                              ('K Nearest Neighbours',
##                               KNeighborsClassifier(n_neighbors=27)),
##                              ('Classification Tree',
##                               DecisionTreeClassifier(min_samples_leaf=0.13,
##                                                      random_state=1))])
## 
## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/linear_model/_logistic.py:814: ConvergenceWarning: lbfgs failed to converge (status=1):
## STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
## 
## Increase the number of iterations (max_iter) or scale the data as shown in:
##     https://scikit-learn.org/stable/modules/preprocessing.html
## Please also refer to the documentation for alternative solver options:
##     https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
##   n_iter_i = _check_optimize_result(

    y_pred = vc.predict(X_test)

# Calculate accuracy score

    ## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/base.py:441: UserWarning: X does not have valid feature names, but KNeighborsClassifier was fitted with feature names
##   warnings.warn(

    accuracy = accuracy_score(y_test, y_pred)
print('Voting Classifier: {:.3f}'.format(accuracy))

    ## Voting Classifier: 0.690

    Great work! Notice how the voting classifier achieves a test set accuracy of 76.4%. This value is greater than that achieved by LogisticRegression.