Bagging and Random Forests#

Bagging is an ensemble method involving training the same algorithm many times using different subsets sampled from the training data. In this chapter, you’ll understand how bagging can be used to create a tree ensemble. You’ll also learn how the random forests algorithm can lead to further ensemble diversity through randomization at the level of each split in the trees forming the ensemble.

Bagging#

Define the bagging classifier#

In the following exercises you’ll work with the Indian Liver Patient dataset from the UCI machine learning repository. Your task is to predict whether a patient suffers from a liver disease using 10 features including Albumin, age and gender. You’ll do so using a Bagging Classifier.

  • Import DecisionTreeClassifier from sklearn.tree and BaggingClassifier from sklearn.ensemble.
  • Instantiate a DecisionTreeClassifier called dt.
  • Instantiate a BaggingClassifier called bc consisting of 50 trees. 
    • # Import DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier

# Import BaggingClassifier
from sklearn.ensemble import BaggingClassifier

# Instantiate dt
dt = DecisionTreeClassifier(random_state=1)

# Instantiate bc
bc = BaggingClassifier(base_estimator=dt, n_estimators=50, random_state=1)

    Great! In the following exercise, you’ll train bc and evaluate its test set performance.

    Evaluate Bagging performance#

    Now that you instantiated the bagging classifier, it’s time to train it and evaluate its test set accuracy.

    The Indian Liver Patient dataset is processed for you and split into 80% train and 20% test. The feature matrices X_train and X_test, as well as the arrays of labels y_train and y_test are available in your workspace. In addition, we have also loaded the bagging classifier bc that you instantiated in the previous exercise and the function accuracy_score() from sklearn.metrics.

  • Fit bc to the training set.
  • Predict the test set labels and assign the result to y_pred.
  • Determine bc’s test set accuracy. 
    • # Fit bc to the training set
bc.fit(X_train, y_train)

# Predict test set labels

    ## BaggingClassifier(base_estimator=DecisionTreeClassifier(random_state=1),
##                   n_estimators=50, random_state=1)

    y_pred = bc.predict(X_test)

# Evaluate acc_test
acc_test = accuracy_score(y_test, y_pred)
print('Test set accuracy of bc: {:.2f}'.format(acc_test)) 

    ## Test set accuracy of bc: 0.70

    Great work! A single tree dt would have achieved an accuracy of 63% which is 4% lower than bc’s accuracy!

    Out of Bag Evaluation#

    Prepare the ground#

    In the following exercises, you’ll compare the OOB accuracy to the test set accuracy of a bagging classifier trained on the Indian Liver Patient dataset.

    In sklearn, you can evaluate the OOB accuracy of an ensemble classifier by setting the parameter oob_score to True during instantiation. After training the classifier, the OOB accuracy can be obtained by accessing the .oob_score\_ attribute from the corresponding instance.

    In your environment, we have made available the class DecisionTreeClassifier from sklearn.tree.

  • Import BaggingClassifier from sklearn.ensemble.
  • Instantiate a DecisionTreeClassifier with min_samples_leaf set to 8.
  • Instantiate a BaggingClassifier consisting of 50 trees and set oob_score to True. 
    • # Import DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier

# Import BaggingClassifier
from sklearn.ensemble import BaggingClassifier

# Instantiate dt
dt = DecisionTreeClassifier(min_samples_leaf=8, random_state=1)

# Instantiate bc
bc = BaggingClassifier(base_estimator=dt, 
            n_estimators=50,
            oob_score=True,
            random_state=1)

    Great! In the following exercise, you’ll train bc and compare its test set accuracy to its OOB accuracy.

    OOB Score vs Test Set Score#

    Now that you instantiated bc, you will fit it to the training set and evaluate its test set and OOB accuracies.

    The dataset is processed for you and split into 80% train and 20% test. The feature matrices X_train and X_test, as well as the arrays of labels y_train and y_test are available in your workspace. In addition, we have also loaded the classifier bc instantiated in the previous exercise and the function accuracy_score() from sklearn.metrics.

  • Fit bc to the training set and predict the test set labels and assign the results to y_pred.
  • Evaluate the test set accuracy acc_test by calling accuracy_score.
  • Evaluate bc’s OOB accuracy acc_oob by extracting the attribute oob_score\_ from bc. 
    • # Fit bc to the training set 
bc.fit(X_train, y_train)

# Predict test set labels

    ## BaggingClassifier(base_estimator=DecisionTreeClassifier(min_samples_leaf=8,
##                                                         random_state=1),
##                   n_estimators=50, oob_score=True, random_state=1)

    y_pred = bc.predict(X_test)

# Evaluate test set accuracy
acc_test = accuracy_score(y_test, y_pred)

# Evaluate OOB accuracy
acc_oob = bc.oob_score_

# Print acc_test and acc_oob
print('Test set accuracy: {:.3f}, OOB accuracy: {:.3f}'.format(acc_test, acc_oob))

    ## Test set accuracy: 0.690, OOB accuracy: 0.687

    Great work! The test set accuracy and the OOB accuracy of bc are both roughly equal to 70%!

    Random Forests (RF)#

    Train an RF regressor#

    In the following exercises you’ll predict bike rental demand in the Capital Bikeshare program in Washington, D.C using historical weather data from the Bike Sharing Demand dataset available through Kaggle. For this purpose, you will be using the random forests algorithm. As a first step, you’ll define a random forests regressor and fit it to the training set.

    The dataset is processed for you and split into 80% train and 20% test. The features matrix X_train and the array y_train are available in your workspace.

  • Import RandomForestRegressor from sklearn.ensemble.
  • Instantiate a RandomForestRegressor called rf consisting of 25 trees.
  • Fit rf to the training set. 
    • # Import RandomForestRegressor
from sklearn.ensemble import RandomForestRegressor

# Instantiate rf
rf = RandomForestRegressor(n_estimators=25,
            random_state=2)
            
# Fit rf to the training set    
rf.fit(X_train, y_train) 

    ## RandomForestRegressor(n_estimators=25, random_state=2)

    Great work! Next comes the test set RMSE evaluation part.

    Evaluate the RF regressor#

    You’ll now evaluate the test set RMSE of the random forests regressor rf that you trained in the previous exercise.

    The dataset is processed for you and split into 80% train and 20% test. The features matrix X_test, as well as the array y_test are available in your workspace. In addition, we have also loaded the model rf that you trained in the previous exercise.

  • Import mean_squared_error from sklearn.metrics as MSE.
  • Predict the test set labels and assign the result to y_pred.
  • Compute the test set RMSE and assign it to rmse_test. 
    • # Import mean_squared_error as MSE
from sklearn.metrics import mean_squared_error as MSE

# Predict the test set labels
y_pred = rf.predict(X_test)

# Evaluate the test set RMSE
rmse_test = MSE(y_test,y_pred)**0.5

# Print rmse_test
print('Test set RMSE of rf: {:.2f}'.format(rmse_test))

    ## Test set RMSE of rf: 0.43

    Great work! You can try training a single CART on the same dataset. The test set RMSE achieved by rf is significantly smaller than that achieved by a single CART!

    Visualizing features importances#

    In this exercise, you’ll determine which features were the most predictive according to the random forests regressor rf that you trained in a previous exercise.

    For this purpose, you’ll draw a horizontal barplot of the feature importance as assessed by rf. Fortunately, this can be done easily thanks to plotting capabilities of pandas.

    We have created a pandas.Series object called importances containing the feature names as index and their importances as values. In addition, matplotlib.pyplot is available as plt and pandas as pd.

  • Call the .sort_values() method on importances and assign the result to importances_sorted.

  • Call the .plot() method on importances_sorted and set the arguments:

  • kind to ‘barh’
  • color to ‘lightgreen’ 
    • # Create a pd.Series of features importances
importances = pd.Series(data=rf.feature_importances_,
                        index= X_train.columns)

# Sort importances
importances_sorted = importances.sort_values()

# Draw a horizontal barplot of importances_sorted
importances_sorted.plot(kind='barh', color='lightgreen')
plt.title('Features Importances')
plt.show()

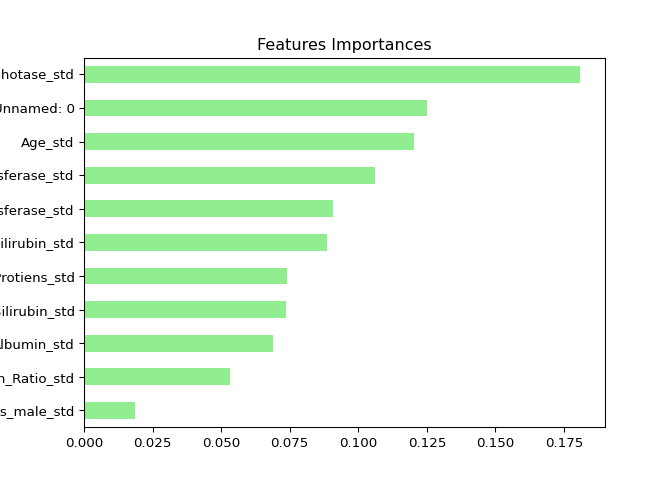
    Apparently, hr and workingday are the most important features according to rf. The importances of these two features add up to more than 90%!