Loss functions#

In this chapter you will discover the conceptual framework behind logistic regression and SVMs. This will let you delve deeper into the inner workings of these models.

Linear classifiers: the coefficients#

How models make predictions#

Which classifiers make predictions based on the sign (positive or negative) of the raw model output?

  • Logistic regression only

  • Linear SVMs only

  • Neither

  • Both logistic regression and Linear SVMs

Nice! Furthermore, since logistic regression and SVMs are both linear classifiers, the raw model output is a linear function of x.

Changing the model coefficients#

When you call fit with scikit-learn, the logistic regression coefficients are automatically learned from your dataset. In this exercise you will explore how the decision boundary is represented by the coefficients. To do so, you will change the coefficients manually (instead of with fit), and visualize the resulting classifiers.

A 2D dataset is already loaded into the environment as X and y, along with a linear classifier object model.

  • Set the two coefficients and the intercept to various values and observe the resulting decision boundaries.
  • Try to build up a sense of how the coefficients relate to the decision boundary.
  • Set the coefficients and intercept such that the model makes no errors on the given training data. 
    • # edited/added
X = np.array([[ 1.78862847,  0.43650985],
       [ 0.09649747, -1.8634927 ],
       [-0.2773882 , -0.35475898],
       [-3.08274148,  2.37299932],
       [-3.04381817,  2.52278197],
       [-1.31386475,  0.88462238],
       [-2.11868196,  4.70957306],
       [-2.94996636,  2.59532259],
       [-3.54535995,  1.45352268],
       [ 0.98236743, -1.10106763],
       [-1.18504653, -0.2056499 ],
       [-1.51385164,  3.23671627],
       [-4.02378514,  2.2870068 ],
       [ 0.62524497, -0.16051336],
       [-3.76883635,  2.76996928],
       [ 0.74505627,  1.97611078],
       [-1.24412333, -0.62641691],
       [-0.80376609, -2.41908317],
       [-0.92379202, -1.02387576],
       [ 1.12397796, -0.13191423]])
y = np.array([-1, -1, -1,  1,  1, -1,  1,  1,  1, -1, -1,  1,  1, -1,  1, -1, -1,
       -1, -1, -1])
model = LogisticRegression()
model.fit(X, y)

# Set the coefficients

    ## LogisticRegression()

    model.coef_ = np.array([[-1,1]])
model.intercept_ = np.array([-3])

# Plot the data and decision boundary
plot_classifier(X,y,model)

# Print the number of errors

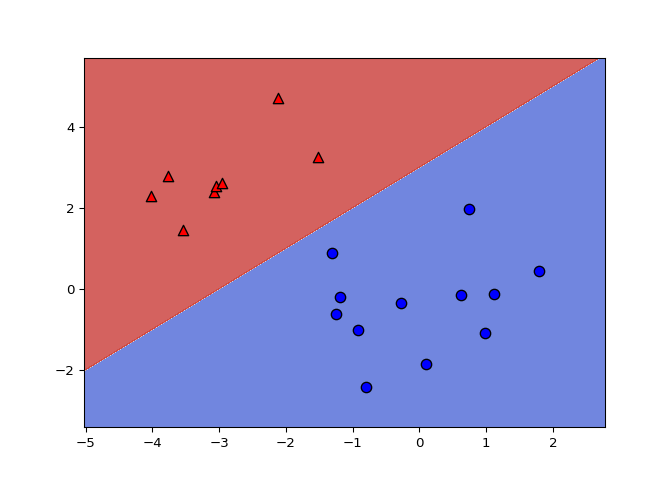
    num_err = np.sum(y != model.predict(X))
print("Number of errors:", num_err)

    ## Number of errors: 0

    Great job! As you’ve been experiencing, the coefficients determine the slope of the boundary and the intercept shifts it.

    What is a loss function?#

    The 0-1 loss#

    • Least squares: the squared loss

      • scikit-learn’s LinearRegression minimizes a loss: $\(\sum\_{i=1}^{n}(\text{true ith target value - predicted ith target value})^2\)$

      • Minimization is with respect to coefficients or parameters of the model.

    • Classification errors: the 0-1 loss

      • Squared loss not appropriate for classification problems

      • A natrual loss for classification problem is the number of errors

      • This is the 0-1 loss: it’s 0 for a correct prediction and 1 for an incorrect prediction

      • But this loss is hard to minimize

    In the figure below, what is the 0-1 loss (number of classification errors) of the classifier?

    • 0

    • 1

    • 2

    • 3

    Correct! There is 1 misclassified red point and 1 misclassified blue point.

    Minimizing a loss function#

    In this exercise you’ll implement linear regression “from scratch” using scipy.optimize.minimize.

    We’ll train a model on the Boston housing price data set, which is already loaded into the variables X and y. For simplicity, we won’t include an intercept in our regression model.

  • Fill in the loss function for least squares linear regression.
  • Print out the coefficients from fitting sklearn’s LinearRegression. 
    • # edited/added
import pandas as pd
from scipy.optimize import minimize
from sklearn.linear_model import LinearRegression
X = pd.read_csv('archive/Linear-Classifiers-in-Python/datasets/boston_X.csv').to_numpy()
y = pd.read_csv('archive/Linear-Classifiers-in-Python/datasets/boston_y.csv').to_numpy()

# The squared error, summed over training examples
def my_loss(w):
    s = 0
    for i in range(y.size):
        # Get the true and predicted target values for example 'i'
        y_i_true = y[i]
        y_i_pred = w@X[i]
        s = s + (y_i_true - y_i_pred)**2
    return s
  
# Returns the w that makes my_loss(w) smallest
w_fit = minimize(my_loss, X[0]).x
print(w_fit)

# Compare with scikit-learn's LinearRegression coefficients

    ## [-9.16299769e-02  4.86754601e-02 -3.77616187e-03  2.85635921e+00
##  -2.88073141e+00  5.92521965e+00 -7.22450907e-03 -9.67993759e-01
##   1.70448640e-01 -9.38968004e-03 -3.92422032e-01  1.49830751e-02
##  -4.16972374e-01]

    lr = LinearRegression(fit_intercept=False).fit(X,y)
print(lr.coef_)

    ## [[-9.16297843e-02  4.86751203e-02 -3.77930006e-03  2.85636751e+00
##   -2.88077933e+00  5.92521432e+00 -7.22447929e-03 -9.67995240e-01
##    1.70443393e-01 -9.38925373e-03 -3.92425680e-01  1.49832102e-02
##   -4.16972624e-01]]

    Great job! This was a tough one. Isn’t it cool how you reproduce the weights learned by scikit-learn?

    Loss function diagrams#

    Classification loss functions#

    Which of the four loss functions makes sense for classification?

    • (1)

    • (2)

    • (3)

    • (4)

    Correct! This loss is very similar to the hinge loss used in SVMs (just shifted slightly).

    Comparing the logistic and hinge losses#

    In this exercise you’ll create a plot of the logistic and hinge losses using their mathematical expressions, which are provided to you.

    The loss function diagram from the video is shown on the right.

  • Evaluate the log_loss() and hinge_loss() functions at the grid points so that they are plotted. 
    • # Mathematical functions for logistic and hinge losses
def log_loss(raw_model_output):
   return np.log(1+np.exp(-raw_model_output))
def hinge_loss(raw_model_output):
   return np.maximum(0,1-raw_model_output)

# Create a grid of values and plot
grid = np.linspace(-2,2,1000)
plt.plot(grid, log_loss(grid), label='logistic')
plt.plot(grid, hinge_loss(grid), label='hinge')
plt.legend()
plt.show()

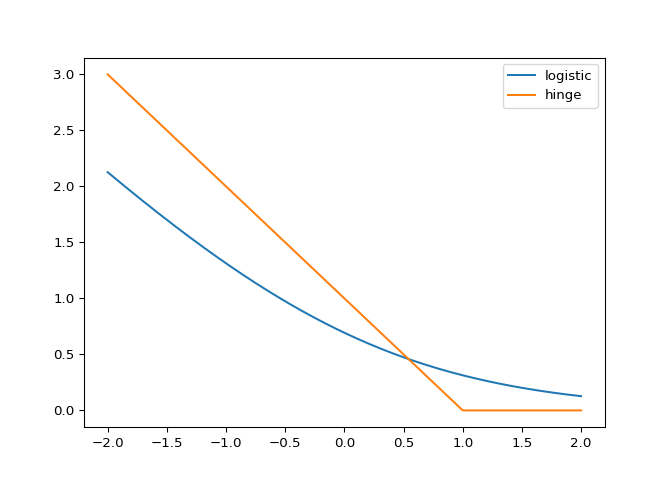
    Nice! As you can see, these match up with the loss function diagrams we saw in the video.

    Implementing logistic regression#

    This is very similar to the earlier exercise where you implemented linear regression “from scratch” using scipy.optimize.minimize. However, this time we’ll minimize the logistic loss and compare with scikit-learn’s LogisticRegression (we’ve set C to a large value to disable regularization; more on this in Chapter 3!).

    The log_loss() function from the previous exercise is already defined in your environment, and the sklearn breast cancer prediction dataset (first 10 features, standardized) is loaded into the variables X and y.

  • Input the number of training examples into range().
  • Fill in the loss function for logistic regression.
  • Compare the coefficients to sklearn’s LogisticRegression. 
    • # edited/added
X = pd.read_csv('archive/Linear-Classifiers-in-Python/datasets/breast_X.csv').to_numpy()
y = pd.read_csv('archive/Linear-Classifiers-in-Python/datasets/breast_y.csv').to_numpy()

# The logistic loss, summed over training examples
def my_loss(w):
    s = 0
    for i in range(y.size):
        raw_model_output = w@X[i]
        s = s + log_loss(raw_model_output * y[i])
    return s
  
# Returns the w that makes my_loss(w) smallest
w_fit = minimize(my_loss, X[0]).x
print(w_fit)

# Compare with scikit-learn's LogisticRegression

    ## [ 1.03608522 -1.65378403  4.08314729 -9.40923525 -1.06786728  0.0789288
##  -0.85110209 -2.44102633 -0.4528562   0.43353478]

    lr = LogisticRegression(fit_intercept=False, C=1000000).fit(X,y)

    ## /Users/macos/Library/r-miniconda/envs/r-reticulate/lib/python3.8/site-packages/sklearn/utils/validation.py:985: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
##   y = column_or_1d(y, warn=True)

    print(lr.coef_)

    ## [[ 1.03665946 -1.65380077  4.08233062 -9.40904867 -1.06787935  0.07901598
##   -0.85099843 -2.44107473 -0.45288928  0.43348202]]

    Great job! As you can see, logistic regression is just minimizing the loss function we’ve been looking at. Much more on logistic regression in the next chapter!